Trasformare gradi in radianti e radianti in gradi: come fare e cosa sapere
Hai bisogno di una mano con la
trigonometria? Proprio non ti piace o ci sono dei concetti che non riesci a capire? Dopo avere visto come misurare gli
angoli in gradi e come misurarli in
radianti, è arrivato il momento di capire quali sono le
formule per passare da una misura in gradi ad una in radianti (e viceversa) dell’ampiezza di un angolo. Perché conoscere la differenza tra gradi e radianti e come fare per convertire il tipo di misurazione? È fondamentale conoscere bene queste le formule di conversione da una unità di misura all’altra per potere affrontare lo studio della trigonometria. Pronto allora ad affrontare questo viaggio alla scoperta delle
formule di conversione dei gradi in radianti e viceversa?
Convertire un angolo da gradi a radianti e viceversa: cosa imparerai oggi
Dopo la lettura seguente, sarai in grado di passare da un sistema di misura in gradi ad un sistema di misura in radianti per calcolare l’ampiezza di un angolo. Queste nozioni ti saranno davvero utili per lo studio della trigonometria.
Cosa devi sapere:
Suggerimento:
- procurati dei fogli a quadretti e durante la lettura prova a riprodurre i disegni geometrici che trovi di seguito e scrivi anche le formule presenti
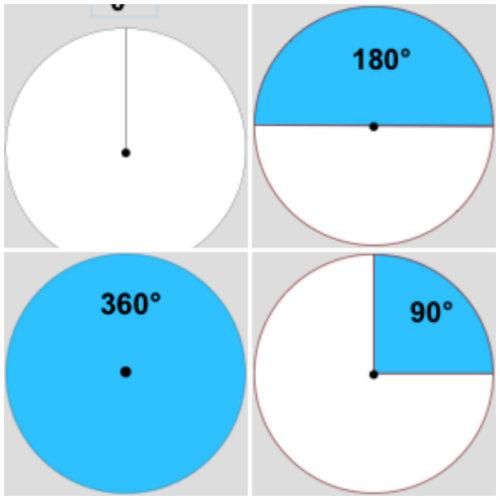
Come convertire gradi in radianti e viceversa
Per passare da un sistema di misura in gradi ad una misura in radianti e viceversa si usano le cosiddette
proporzioni matematiche.
Poiché conosciamo i valori in gradi ed in radianti dei cosiddetti
angoli notevoli possiamo utilizzare la seguente proporzione matematica:
La formula precedente si legge
l’angolo alfa misurato in gradi sta a 360° come l’angolo alfa misurato in radianti sta a 2 Pi greco
Passaggio da gradi a radianti
Supponiamo di conoscere la misura di un angolo
alfa in gradi: quale sarà la misura di
alfa in rad? Dalla formula precedente e per le proprietà delle proporzioni abbiamo che
Esempio 1: passaggio da gradi a radianti
Supponiamo di avere
alfa=66°: vogliamo calcolare la sua misura in radianti. Applicando la formula riportata sopra abbiamo
Osserva che nel caso della misura in rad è buona regola lasciare sempre il fattore numerico Pi greco perché questo semplifica moltissimo le cose quando si affronta lo studio della trigonometria.
Passaggio da radianti a gradi
Se invece conosciamo la misura di un angolo
alfa in radianti, la sua misura in gradi sarà
Esempio 2: passaggio da radianti a gradi
Supponiamo di avere
: vogliamo calcolare la sua misura in gradi.
Applicando la formula riportata sopra abbiamo
Conversione gradi in radianti e viceversa: riepilogo
Avere dimestichezza con la misura degli angoli in gradi e radianti è fondamentale per affrontare lo studio della Trigonometria. La misura in gradi è sicuramente quella più nota, ma la misura in radianti è sicuramente più usata, perché semplifica moltissimo i passaggi negli esercizi. È importante imparare e ricordare le formule di conversione per passare dalla misura in gradi a quella in radianti.
