Circonferenza goniometrica: definizione e come disegnarla

Cos'è la circonferenza goniometrica e come disegnarla

Iniziamo il nostro viaggio alla scoperta della trigonometria! Questo particolare ramo della matematica, infatti, mette spesso in crisi gli studenti che non riescono a capirne l'utilità, ma soprattutto fanno fatica a destreggiarsi tra seno, coseno, tangenti e a risolvere esercizi e problemi di trigonometria. Hai bisogno di un aiuto per riuscire finalmente a capire la trigonometria e le sue formule e superare i compiti in classe con buoni voti (o almeno raggiungere la sufficienza)? Noi di ScuolaZoo stiamo creando una guida completa a tutti gli argomenti di trigonometria. È quindi arrivato il momento di iniziare: in questo primo articolo, ti spieghiamo cos’è la circonferenza goniometrica, spesso indicata anche come circonferenza unitaria, un concetto che devi conoscere bene per iniziare lo studio della Trigonometria.

Circonferenza goniometrica: cosa imparerai oggi

Dopo la lettura di questo articolo, sarai in grado di disegnare, dire cos’è e a cosa serve la circonferenza goniometrica. Cosa devi sapere:

• cos’è un angolo
• piano e coordinate cartesiane
• Teorema di Pitagora

Suggerimento:

• procurati dei fogli a quadretti e durante la lettura prova a riprodurre i disegni geometrici che trovi di seguito.

 

Circonferenza goniometrica: definizione e come disegnarla

Per non fare confusione, iniziamo subito dalle basi e quindi impariamo la definizione di circonferenza goniometrica e cerchiamo di capire insieme come si disegna.

Definizione di cironferenza goniometrica

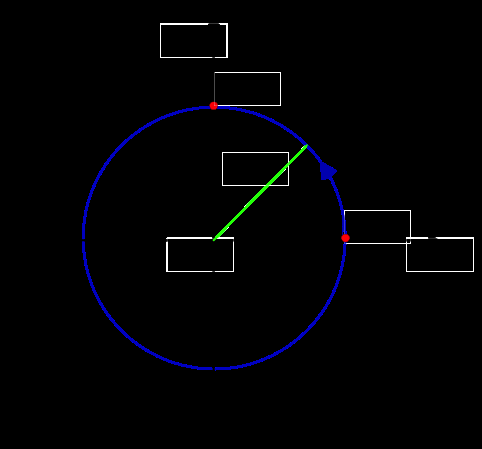
La circonferenza goniometrica (detta anche circonferenza unitaria) è una circonferenza disegnata nel piano cartesiano xy con raggio r uguale ad 1 (da qui circonferenza unitaria). Il centro della circonferenza unitaria coincide con l’origine degli assi del piano cartesiano. Sulla circonferenza goniometrica viene anche fissato il verso antiorario come verso positivo.

Come disegnare una circonferenza goniometrica

Essendo r=1, abbiamo, ad esempio, che il punto A sul piano cartesiano avrà coordinate (1,0), il punto B avrà coordinate (0,1). Se disegniamo un qualsiasi raggio r della circonferenza, il raggio incontra un generico punto P sulla circonferenza di coordinate (xP, yP).  

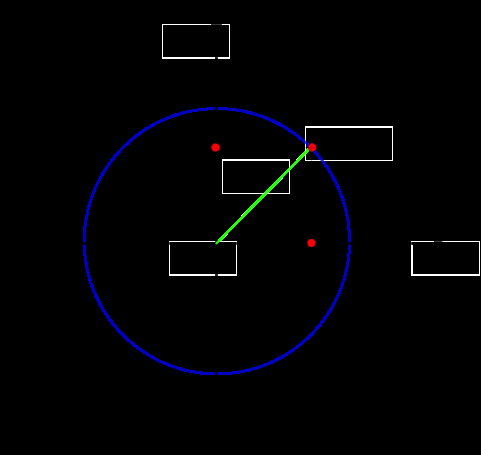
Circonferenza gonimetrica: formule

Osserviamo che il triangolo OPH è un triangolo rettangolo (l’angolo OHP=90°) e quindi applicando il Teorema di Pitagora ai cateti OH, PH ed all’ipotenusa OP abbiamo OH² + PH² = OP² => x_P² + y_P² = r² => x_P² + y_P² = 1 Osservazione 1: In una circonferenza goniometrica la somma dei quadrati delle coordinate di un punto P, appartenente alla circonferenza stessa, è uguale ad 1. Disegnando un generico raggio r, osserviamo che individuiamo anche un angolo che in figura abbiamo indicato con q, con origine in O e delimitato dal raggio r e dall’asse x.

Circonferenza goniometrica: gli angoli

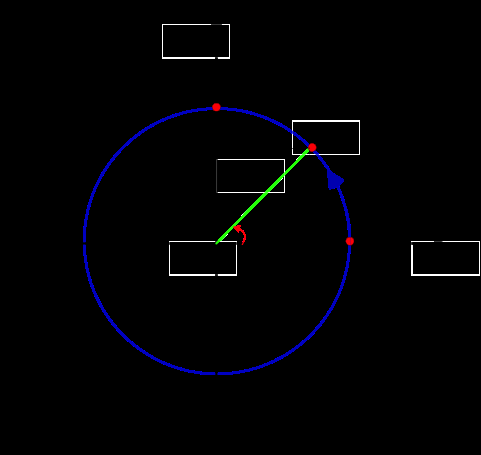
La circonferenza goniometrica mi permette di disegnare angoli sul piano cartesiano xy. Sulla circonferenza goniometrica è possibile individuare degli angoli che hanno dei valori “particolari”: 0°, 90°, 180°, 270°, 360°. Questi angoli sono detti angoli notevoli della circonferenza goniometrica.  

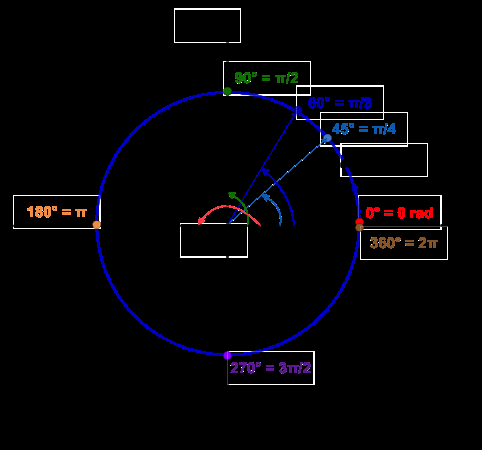
Trigonometria, la circonferenza unitaria: riepilogo

In breve, ecco cosa devi tenere sempre a mente:

• La circonferenza goniometrica consente di disegnare angoli sul piano cartesiano.
• È detta anche circonferenza unitaria, in quanto il suo raggio è uguale ad 1. Sulla circonferenza goniometrica è possibile individuare degli angoli che vengono detti angoli notevoli.
• Tutti i punti della circonferenza godono della proprietà che la somma dei quadrati delle loro coordinate è uguale ad 1.