Misura degli angoli in radianti: definizioni e cosa sapere

Cosa sapere sulla misura di un angolo in radianti

La geometria è il tallone d'Achille di numerosi studenti: hai problemi soprattutto con la misurazione degli angoli? Tranquillo: quando si parla di circonferenze, gradi e radianti sono in molti coloro che vanno nel panico. In realtà, imparare come si misurano gli angoli, anche in radianti, è più facile di quanto possa sembrare! Pronto per affrontare una nuova lezione di trigonometria? Di seguito imparerai come si misura l’ampiezza di un angolo in radianti, un'unità di misura alternativa ai gradi, che è  fondamentale conoscere bene prima di affrontare lo studio della Trigonometria. Vuoi sapere invece come si passa da radianti a gradi o viceversa? Non perdere:

• Convertire i gradi in radianti e viceversa

Misura di un angolo in radianti: cosa imparerai oggi

Dopo la lettura seguente sarai in grado di dire cosa sono i radianti e come si misura l’ampezza di un angolo. Queste nozioni ti saranno davvero utili per lo studio della trigonometria. Cosa devi sapere:

• cos’è un angolo
• misura di un angolo in gradi (°)
• la misura C di una circonferenza di raggio r ()

Suggerimento:

• procurati dei fogli a quadretti e durante la lettura prova a riprodurre i disegni geometrici che trovi di seguito e scrivi anche le formule presenti

Radianti: significato e spiegazione

I radianti sono una unità di misura per calcolare l’ampiezza degli angoli, forse meno conosciuta rispetto ai gradi, ma davvero utile in trigonometria per la semplificazione delle formule, in quanto la misura degli angoli è espressa da numeri puri, ossia numeri senza alcuna unità di misura. Consideriamo una circonferenza di centro O e raggio r e consideriamo due semirette (con origine in O) che intercettano sulla circonferenza un arco l e delimitano un angolo alfa. 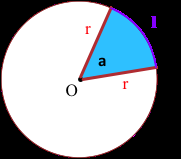La misura in radianti dell’angolo alfa è data dal rapporto tra lunghezza dell’arco l (intercettato sulla circonferenza dai lati dell’angolo) ed il raggio r della circonferenza stessa, ossia Come dicevamo prima il radiante è un numero puro, cioè adimensionale, in quanto dato dal rapporto tra due lunghezze. Calcoliamo le misure degli angoli notevoli in radianti:

• Angolo giro, (360°) in radianti misura 2 Pi greco

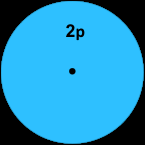
Partendo dalla definizione di radiante (vedi formula precedente) e considerando che nel caso di angolo giro l’arco l individuato sulla circonferenza è tutta la circonferenza stessa, ossia abbiamo che

• Angolo piatto, (180°) in radianti misura Pi greco

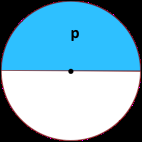
Anche in questo caso partendo dalla definizione di radiante e considerando che nel caso di angolo piatto l’arco l individuato sulla circonferenza è la metà della circonferenza stessa, ossia  abbiamo che

• Angolo retto (90°) in radianti misura

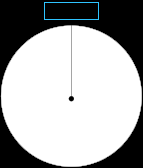
Nel caso dell’angolo retto l’arco l individuato sulla circonferenza è un quarto dell’intera circonferenza, ossia  e quindi abbiamo che

• Angolo nullo (0°) in radianti misura 0

Infatti per l’angolo nullo abbiamo l=0, da cui Osservazione: nel caso della misura in rad è buona regola lasciare sempre il fattore numerico Pi greco perché questo semplifica moltissimo le cose quando si affronta lo studio della trigonometria.

Misura di un angolo in radianti: cenni storici

I radianti consentono di confrontare angoli e segmenti. Eulero già nella prima metà del 1700 indicava con p un angolo di 180°; tuttavia solo nel 1873 fu usata la parola “radiante” dal matematico James Thomson, fratello del fisico Lord Kelvin, quest’ultimo famoso per i suoi studi in termodinamica…..ma questa è un’altra storia!

Misura di un angolo in radianti: riepilogo

Avere dimestichezza con la misura degli angoli in radianti è fondamentale per affrontare lo studio della Trigonometria. La misura in gradi è sicuramente quella più nota, ma la misura in radianti è sicuramente più usata, perché semplifica moltissimo i passaggi negli esercizi.